Ввести диапазон а б, вывести все совершенные числа — Pascal(Паскаль)

Соверше́нное число́ — натуральное число, равное сумме всех своих собственных делителей (то есть всех положительных делителей, отличных от самого́ числа). Например, число 6 равно сумме своих собственных делителей 1 + 2 + 3. Это понятие было введено пифагорейцами в VI веке до н. э.; согласно их нумерологической мистике, совпадение числа с суммой своих делителей свидетельствовало об особом совершенстве такого числа.

Если суммировать все делители числа (то есть добавить само число) {\displaystyle \sigma (N)-N=N} или {\displaystyle \sigma (N)=2N,} получим другое эквивалентное определение: Совершенные числа — это числа, у которых сумма всех делителей в 2 раза больше самого числа.

По мере того как натуральные числа возрастают, совершенные числа встречаются всё реже. Неизвестно, бесконечно ли множество всех совершенных чисел. Неизвестно также, есть ли среди них нечётные.

Совершенные числа образуют последовательность A000396 в OEIS:

  1. 6,
  2. 28,
  3. 496,
  4. 8128,
  5. 33 550 336,
  6. 8 589 869 056,
  7. 137 438 691 328,
  8. 2 305 843 008 139 952 128,
  9. 2 658 455 991 569 831 744 654 692 615 953 842 176,
  10. 191 561 942 608 236 107 294 793 378 084 303 638 130 997 321 548 169 216,

Примеры чисел

  • 1-е совершенное число — 6 имеет следующие собственные делители: 1, 2, 3; их сумма равна 6.
  • 2-е совершенное число — 28 имеет следующие собственные делители: 1, 2, 4, 7, 14; их сумма равна 28.
  • 3-е совершенное число — 496 имеет следующие собственные делители: 1, 2, 4, 8, 16, 31, 62, 124, 248; их сумма равна 496.
  • 4-е совершенное число — 8128 имеет следующие собственные делители: 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064; их сумма равна 8128.

Алгоритм построения совершенных чисел

Чётные совершенные числа

Алгоритм построения чётных совершенных чисел описан в IX книге Начал Евклида, где было доказано, что число \ 2^{{p-1}}(2^{p}-1) является совершенным, если число \ 2^{p}-1 является простым (т. н. простые числа Мерсенна). Впоследствии Леонард Эйлер доказал, что все чётные совершенные числа имеют вид, указанный Евклидом.

В античные времена были известны только первые четыре совершенных числа (соответствующие р = 2, 3, 5 и 7), они приведены в Арифметике Никомаха Геразского.

Пятое совершенное число 33 550 336, соответствующее р = 13, нашёл в 1536 году голландский математик Худалрик Perиус (лат. Hudalrichus Regius) в трактате «Utriusque Arithmetices» (1536 год). Позднее это число было также обнаружено историками в неопубликованной рукописи Региомонтана 1461 года.

В 1603 году итальянский математик Катальди обнаружил и опубликовал шестое и седьмое совершенные числа: 8 589 869 056 и 137 438 691 328. Они соответствуют р = 17 и р = 19.. Заодно он опроверг гипотезу Никомаха, согласно которой в последних цифрах членов последовательности совершенных чисел чередуются цифры 6 и 8.

В начале XX века были найдены ещё три совершенных числа (для р = 89, 107 и 127). В дальнейшем поиск затормозился вплоть до середины XX века, когда с появлением компьютеров стали возможными вычисления, превосходящие человеческие возможности.

На 2019 год известно 51 совершенное число, вытекающее из простых чисел Мерсенна, поиском которых занимается проект распределённых вычислений GIMPS.

Нечётные совершенные числа

Нечётных совершенных чисел до сих пор не обнаружено, однако не доказано и то, что их не существует. Неизвестно также, конечно ли множество нечётных совершенных чисел, если они существуют.

Доказано, что нечётное совершенное число, если оно существует, превышает 101500; при этом число простых делителей такого числа с учётом кратности не меньше 101. Поиском нечётных совершенных чисел занимается проект распределённых вычислений OddPerfect.org.

Свойства чисел

  • Все чётные совершенные числа (кроме 6) являются суммой кубов последовательных нечётных натуральных чисел

{\displaystyle 1^{3}+3^{3}+5^{3}+\ldots +(2n-1)^{3}=n^{2}(2n^{2}-1)}

  • Все чётные совершенные числа являются треугольными и одновременно шестиугольными числами, то есть, могут быть представлены в виде {\displaystyle n({2n-1})} для некоторого натурального числа n.
  • Сумма всех чисел, обратных делителям совершенного числа (включая само число), равна 2. Это прямое следствие определения и того факта, что сумма делителей при делении на само число дает сумму чисел, обратных делителям.
  • Все совершенные числа являются числами Оре.
  • Все чётные совершенные числа, кроме 6 и 496, заканчиваются в десятичной записи на 16, 28, 36, 56 или 76.
  • Все чётные совершенные числа в двоичной записи содержат сначала p единиц, за которыми следует p-1 нулей (следствие из их общего представления).
  • Если сложить все цифры чётного совершенного числа (кроме 6), затем сложить все цифры полученного числа и так повторять, пока не получится однозначное число, то это число будет равно 1 (2 + 8 = 10, 1 + 0 = 1; 4 + 9 + 6 = 19, 1 + 9 = 10…) Эквивалентная формулировка: остаток от деления чётного совершенного числа, отличного от 6, на 9 равен 1.

Программа

 var
   a,b,s,i:integer;
begin
writeln('Введите диапазон, так 1 5 ');
readln(a,b);
writeln('В результате');
while (a<=b) do
 begin
  s:=0;
  for i:=1 to a-1 do
   if (a mod i=0) then s:=s+i;
  if (s=a) then writeln(a);
  a:=a+1;
 end;
end.

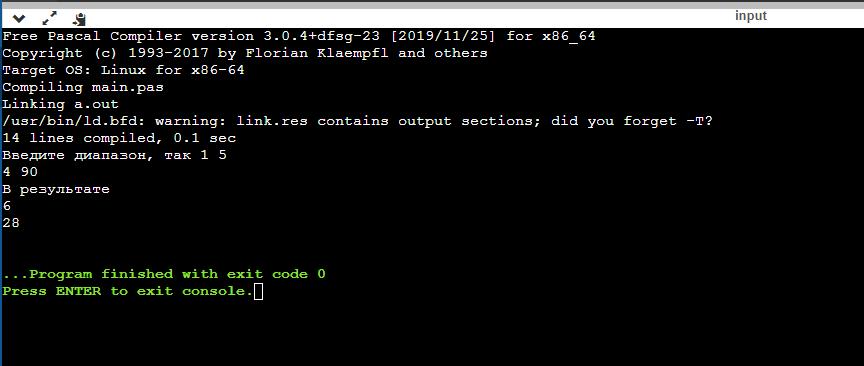
Результат работы программы

Похожие записи/страницы:

Leave a Comment

− 3 = 2