Начнём с того, что любой двумерный массив представляет собой матрицу, т.е. набор чисел, каждое из которых, так сказать, «вставлено» в конкретную ячейку, имеющую свой индивидуальный адрес. Адрес – это два индекса, которые показывают на пересечении какой строки и какого столбца находится тот или иной элемент. Теперь конкретнее. Взгляни на рисунок.
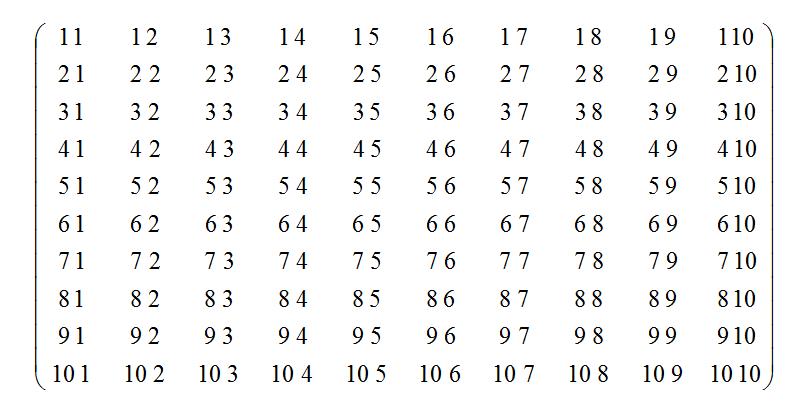
На нём изображена квадратная матрица, т.е. матрица, у которой количество элементов по длине и ширине одинаково. В последующем мы будем пользоваться именно такой из-за её удобства. Это матрица размером 10 на 10 элементов, заполненная не произвольными числами, а индексами (или адресами) элементов. Вот как раз по этим индексам у нас и происходит обращение к элементам массива. Мы можем присваивать им значения, импортировать, сравнивать, производить какие-либо действия и давать им уже новое получившееся значение. Но чтобы все эти операции производить не вручную, а с помощью компьютера, надо выявить определённую закономерность с индексами элементов. Описав последнюю нужным образом и заключив в цикл, мы получим основную часть программы для решения определённой задачи на двумерный массив. Закономерность в 100% случаев заключается в одинаковом соотношении первых и вторых индексов для всех элементов, лежащих в определённом месте, к примеру, выше главной диагонали, на побочной диагонали, сверху от пересечения диагоналей, ну и т.д.
Перейдём к конкретным примерам. Допустим, нам надо найти сумму элементов на главной диагонали. Для начала напомним, что главная диагональ идёт начиная от верхнего левого угла до нижнего правого, а побочная, соответственно, из левого нижнего в правый верхний. Ну так вот, посмотри на первый и второй индекс каждого из элементов, лежащего на главной диагонали. Что ты видишь? Они равны! Поэтому в условии ты можешь смело писать:
if i=j then s:=s+a[i,j] , где s – переменная суммы, i – первый индекс, j – второй индекс.
Ну а теперь без объяснений: просто смотри на рисунок и сверяй.
- Индексы элементов, лежащих на главной диагонали равны (доказано ранее) т.е. i = j
- Первый индекс всех элементов выше главной диагонали меньше второго, т.е. i < j
- Первый индекс всех элементо ниже главной диагонали больше второго, т.е. i > j
- Для элементов побочной диагонали сумма первого и второго индексов равна «нарощенному» на единицу порядку матрицы, т.е. i + j = N+1 ,где N – порядок матрицы. Порядок матрицы – это количество элементов матрицы по вертикали или горизонтали. И элемент матрицы на побочной диагонали в общем виде будет иметь адрес a[i, N+1– i] , где a – название массива.
- Для элементов, находящихся над побочной диагональю должно выполняться равенство: i + j < N+1 ,т.е. в условии надо писать: if i + j <N+1 then …
- Для элементов ниже побочной диагонали в предыдущем неравенстве надо всего лишь сменить знак на противоположный, т.е. здесь у нас будет: i + j > N+1, а в условии: if i + j > N+1 then …
- Для элементов над пересечением диагоналей должны выполняться одновременно два неравенства: i + j < N+1 и i < j , т.е. в программе мы напишем if (i + j<N+1) and (i < j) then … (здесь скобки обязательны)
- Для элементов под пересечением диагоналей знаки обоих предыдущих неравенств должны быть противоположными и будет это выглядеть так: i + j> N+1 и i > j ,или в программе: if (i + j> N+1) and (i > j) then … (здесь скобки обязательны)
- Для элементов, находящихся справа от пересечения диагоналей справедлива закономерность: i + j <N+1 и i > j или в среде Pascal это будет выглядеть так: if (i + j<N+1) and (i >j ) then …
- Для элементов, слева от пересечения диагоналей верно соотношение: i + j >N+1 и i < j ,а в программе это будет отражено как: if (i + j>N+1) and (i < j) then …